This notebook contains material from chemeng316_fluids; content is available on Github.

< B.1 Homework 1 | Contents | B.3 Homework 3 >

B.2 Homework 2

ChE 316 – Chem Eng. Fluid Mechanics – Spring 2024

DUE 31 Jan 2024

I created the illustrations shown below using TinkerCAD. I have created a specific "class" link for TinkerCAD so you can see my designs and create your own to share with the class: https://www.tinkercad.com/joinclass/JR4TQ5ASP

Getting Started: Here is some code to at least get the UnitRegistry and CoolProp modules loaded for you to get started.

try:
    import pint
except:
    !pip install pint
    import pint
finally:
    ur = pint.UnitRegistry()

try:
    import CoolProp.CoolProp as CP
except:
    !pip install CoolProp
    import CoolProp.CoolProp as CP

# we need numpy for constants like pi
# https://numpy.org/doc/stable/reference/constants.html
import numpy as np

# we often use sympy to solve equations
import sympy as sp

Problem 1. A research submarine is design to operate 3 km below the ocean surface. If the interior pressure of the submarine is 1 atm, calculate the total pressure on a 15 cm diameter window? Assume the average density of the ocean water is 1,028 kg/m$^3$.

# YOUR SOLUTION HERE

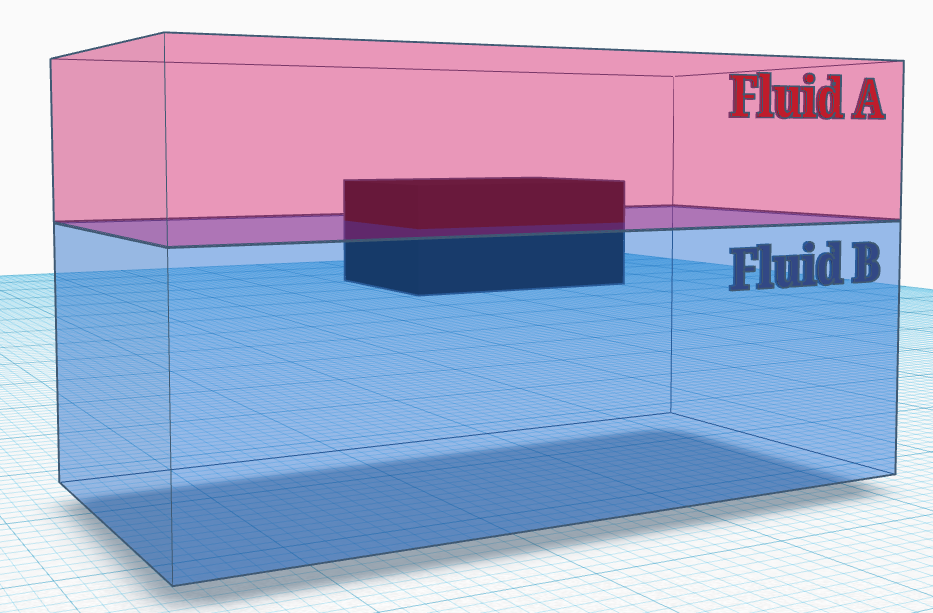
Problem 2. A layer of an unknown liquid A (immiscible with water) floats on top of a layer of water in a beaker. A completely submerged block of specific gravity 0.9 adjusts itself so that its axis is vertical, one-third of its height projects above the unknown/water interface, and two-thirds remain below. What is the specific gravity of A?

# YOUR SOLUTION HERE

Problem 3. Determine the fraction of a 3 inch diameter baseball's volume that is submerged in water if the baseball weighs 5 oz. Assume $\rho_{H20} = 62.4$ lbm/ft$^3$.

# YOUR SOLUTION HERE

< B.1 Homework 1 | Contents | B.3 Homework 3 >